Sodelovanje? (11.-24. nov. 2016 - Piškot)

Teta kriptografija je bila navdušena nad poslanimi rešitvami zadnje naloge (o štirih vodnjakih), saj bi lahko postavila preostala 4 mesta izbrane diagonale vinske kleti, na prva 4 mesta druge diagonale rezervarje za nafto ter na preostala 4 mesta druge diagonale še priključke za elektriko, pa bi še vedno vsak izmed štirih skladnih in povezanih delov tabele 8x8 imel po en vodnjak, eno vinsko klet, en rezervar za nafto ter en priključek za elektriko. Zaskrbelo pa jo je, da je prišlo pri reševanju do pretiranega sodelovanja, saj smo prejeli same enake rešitve (do zrcaljenja ali vrtenja):

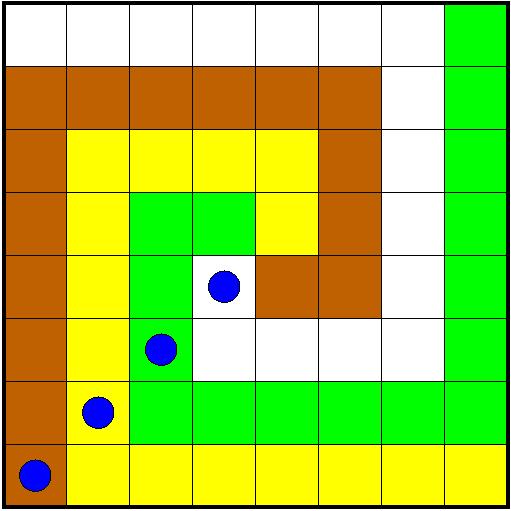
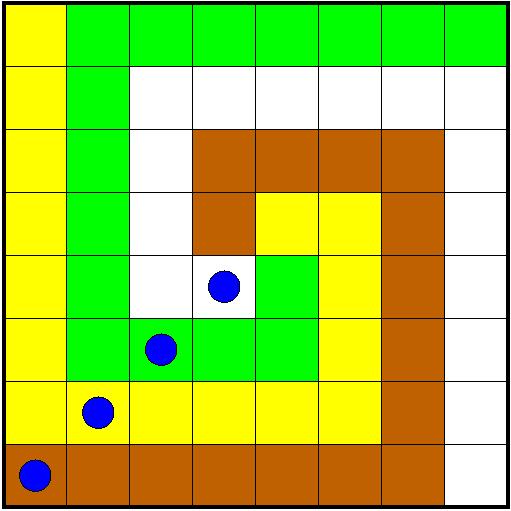
Res, že v primeru n=2 ni težko najti več rešitev. (1) Koliko jih je pravzaprav?

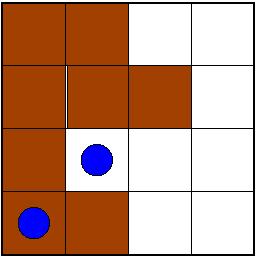
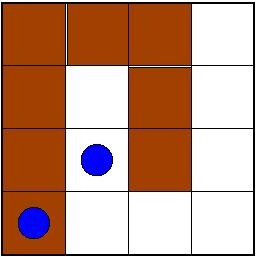
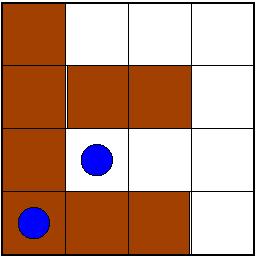
Profesor ji je zagotovil, da tega naši reševalci nikakor ne bi počeli:

• Za pravilno rešitev podelimo le čokolado (če sploh pride do tega),
• pa še te le za prvih nekaj rešitev (saj pazimo na linije reševalcev).
• Le za zelo originalne rešitve imamo na zalogi posebne nagrade.
• Itak pa je bil en izmed reševalcev tudi kolega Demšar.

(2) Bi znali rešiti zagato in bi ponudili kakšen še boljši razlog?

                                                                           #        #       #

Nagajivi hackerji so se tokrat odločili preizkusiti profesorja z "nerešljivim" primerom n=3, tj. tabelo 6x6.
(3) Mar je ta primer res nerešljiv?

Da tudi oni pokažejo dobro voljo, so pripravljeni popustiti pri zahtevi, da se celotna tabla 6x6 razdeli na 3 skladne povezane dele, tako da vsak med njimi vsebuje po en vodnjak (nekaj polj lahko ostane na voljo npr. tudi za otroške mestne parke), medtem, ko naj pogoja o skladnosti in povezanosti vseeno ostaneta.

Tu je primer delitve, pri kateri je vsaka "farma" sestavljena zgolj iz šestih polj:

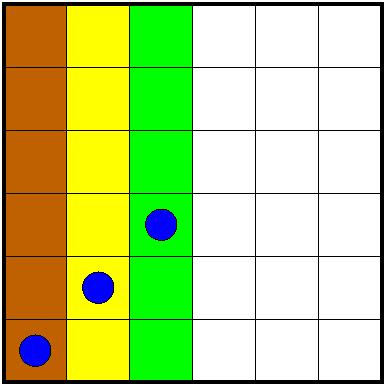
Gotovo to ni najboljša možna velikost farm.

(4) Bi znali najti (naj)boljšo rešitev?
Naiven pristop (npr. z grobo silo) bi bil preveč zamuden (4³³ možnosti).