uganka: Veriga v igri 15 (24. nov. - 8. dec. 2016 - Piškot) - dodani namigi

Odprto: četrtek, 24. november 2016, 00.00

Rok za oddajo: četrtek, 8. december 2016, 09.00

Teti kriptografiji je v roke prišla nova igra, ki jo želi predstaviti študentom FRI:

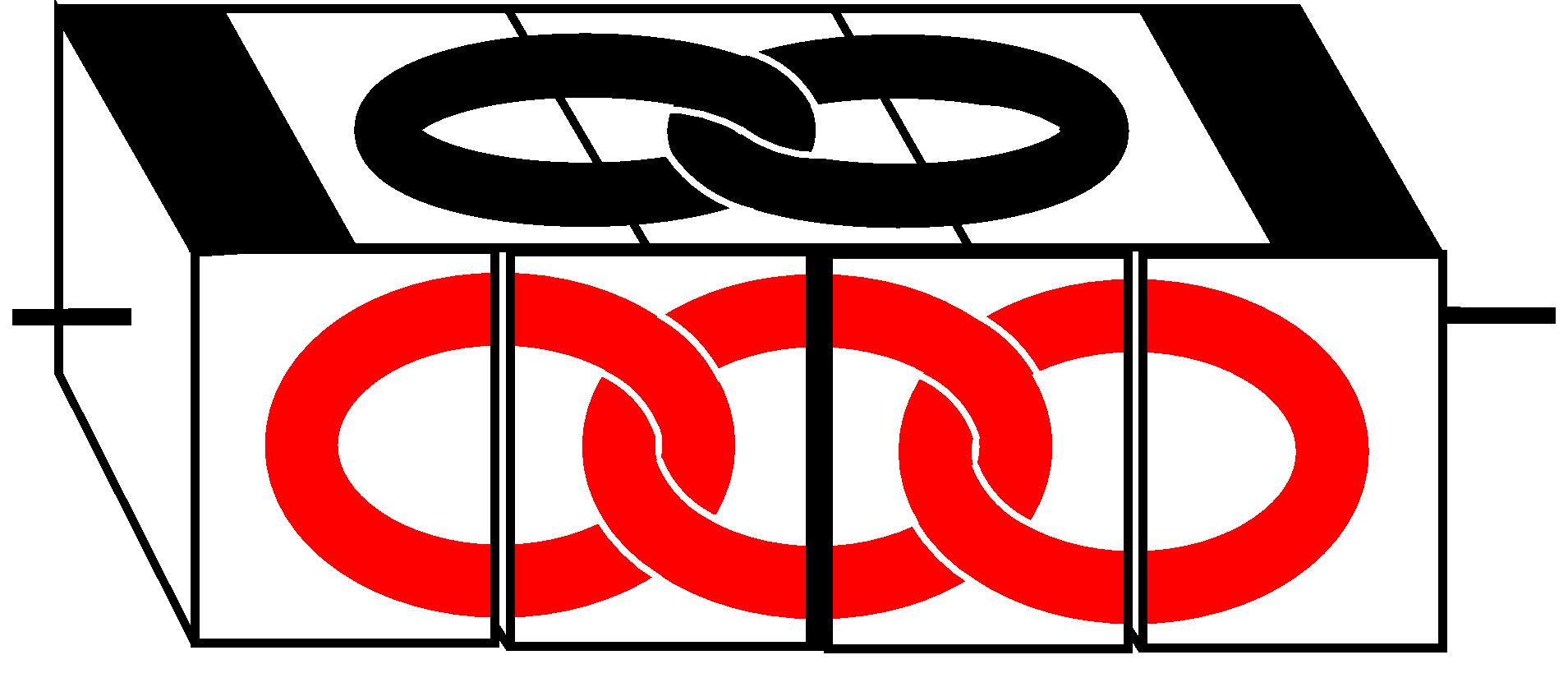
Igra je na prvi pogled podobna Rubikovi kocki, vendar je drugačna. Gre za stolpič, ki je sestavljen iz štirih kock na skupni vertikalni osi, od katerih se zgornja in spodnja vrtita okoli te osi, srednji dve pa sta zlepljeni skupaj, glej sliko.

Vsaka kocka ima spodnjo in zgornjo ploskev, ter štiri stranske. Z izjemo ene stranske ploskve, ki jim matematiki pravijo lica, vsebuje vsaka po eno ploščico, torej jih je skupaj 15 (tako kot pri znameniti igri 15). Poleg omenjenega vrtenja dveh kock, lahko ploščico, ki je nad/pod praznim licem premaknemo nanj.

Ko je igra v začetni poziciji, vidimo na treh straneh po tri rinke (enkrat v rdeči barvi, drugič v zeleni in tretjič v rumeni), na četrti strani pa le dve rinki v črni barvi.

(1) Poiskati je potrebno postopek/algoritem, ki bo premešane ploščice spravil nazaj začetno stanje.

(2) Ali lahko zamenjamo med seboj le ploščice dveh barv, npr. rdeče in zelene ali pa rdeče in rumene?

Namig: En študent je že ugnal/

uganko (pri meni je dobil dejansko igračo), a svoje rešitve še ni zapisal algoritmično (v opravičilo je navedel, da je končal kemijo in je prišel na FRI šele na magisterij). Naša uganka je pravzaprav precej lahka in verjamem, da je naši študentje zaradi sezone kolokvijev v resnici niso niti pretirano reševali (morda tudi ne zaradi tega, ker se jo je težje lotiti brez igrače - čeprav jo lahko igramo s 15imi lističi/kartami ali figurami na šahovski tabli). Pa vendar ste vabljeni, da si preberete Presekova članka o igri 15: Tomaž Pisanski in Sandi Klavžar. Na koncu drugega članka je omenjena nagrada $1000, ki jo je avtor igre 15 ponujal za rešitev zastavljene naloge. Izkazalo se je, da naloga ni rešljiva in so v resnici na račun te igre precej zaslužili prodajalci tablic s ploščicami (pravzaprav služijo nekateri še danes), torej vas na FRI učimo zelo praktične reči.

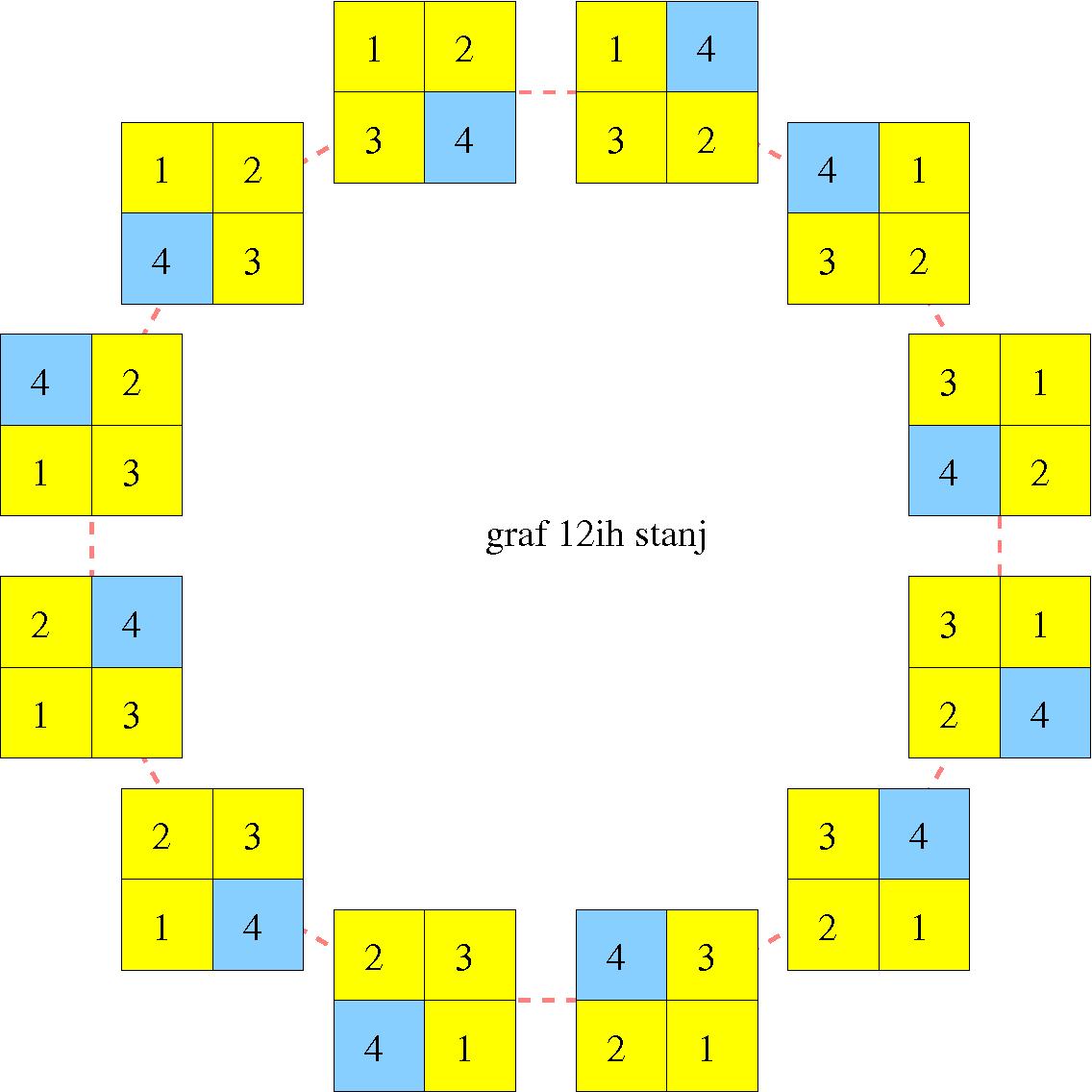
Morda igro bolje razumemo, če si narišemo graf stanj, če seveda le-teh ni preveč (med dvema stanjema vzpostavimo povezavo, če obstaja premik iz enega stanja v drugega, v našem primeru je premik, da potegnemo ploščico na prazno polje ali da obrnemo spodnjo oz. zgornjo kocko). V ta namen posplošimo igro na m stolpcev (na valju) in n vrstic (1. in zadnjo lahko ciklično zamaknemo + transpozicije s praznim poljem (na sliki modro).

Začnimo z najmanjšim primerom: n=m=2 (v tem primeru ni zlepljenih kock na sredini, ciklični zamik prve vrstice pa je enak cikličnemu zamiku druge v nasprotno smer). Koliko je v tem primeru število vseh možnih pozicij/stanj, če zaenkrat še ne uporabljamo cikličnega zamika vrstice, v kateri ni praznega polja? Odg. 4x3!/2 =12, tj. število sodih permutacij štirih elementov oz. 4!/2.

____

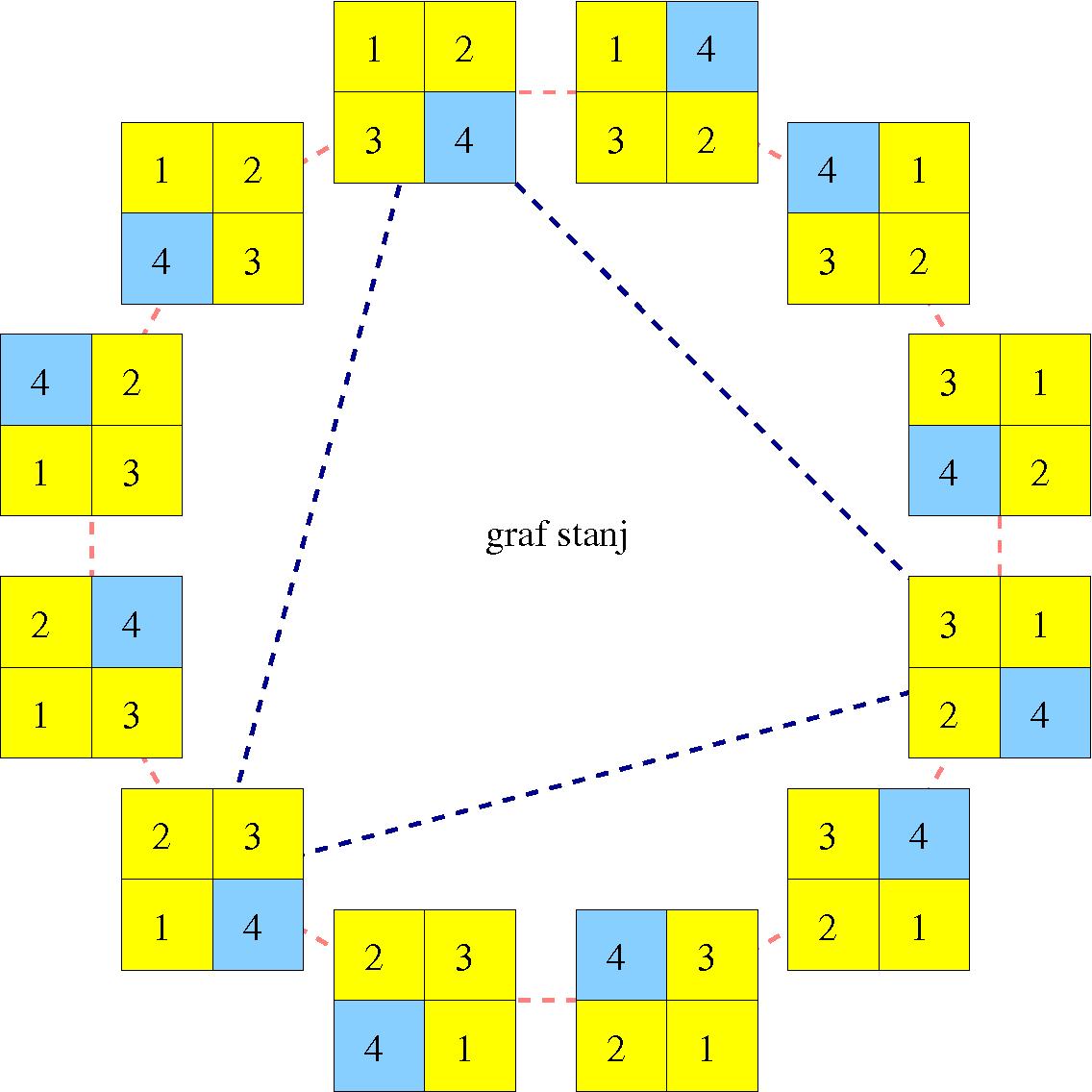
V bistvu nas zanimajo samo tri stanja, tj. tista, ki imajo prazno polje spodaj desno. Le-ta oblikujejo tri-cikel (pri tem modre povezave predstavljajo sestavljeno operacijo). V primeru naše igre dopuščamo še en ciklični zamik, ki ga doslej nismo uporabili. Z njim dosežemo vseh 4!=24 stanj, ... vendar bi tudi tu lahko rekli, da nas zanima le 6 stanj. Le-ta oblikujejo 3 strano prizmo, kar pomeni, da so pri naši igri dosegljiva prav vsa stanja (3!), tj. vse permutacije treh ploščic:

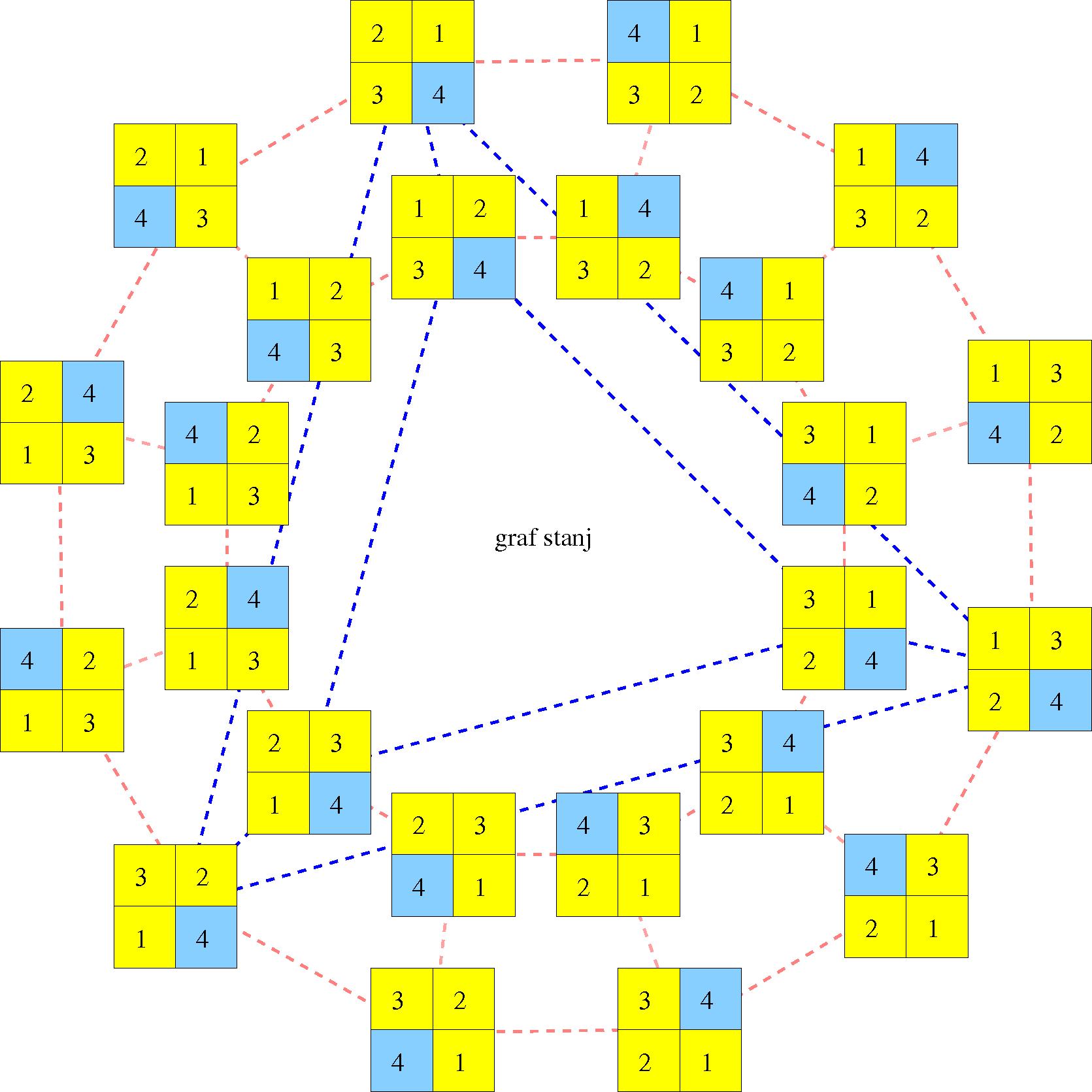
Bi znali analizirati igro v primeru, ko povečamo bodisi m ali n?