Novoletna slikarska kolonija

0. Priprava

• Da boste lahko reševali naloge, si morate namestiti PyQt. Če se kaj zaplete, pišite, pošljite kako sliko zaslona, pa bomo poskusili pomagati.
• Poleg tega si morate pobrati modul risar in ga skopirati v direktorij, v katerem boste imeli svoje programe.
• Napišite program

import risar
risar.stoj()

Pojaviti se mora prazno okno z naslovom Janezovo zasilno platno. Program se "konča", ko zaprete to okno.

1. Črte

Tole je za spoznavanje modula risar. Ogrevanje; potrebovali boste le zanke.

Risar ima med drugim funkcije

• risar.crta(x0, y0, x1, y1, sirina=1, barva=risar.bela), ki nariše črto med podanima koordinatama. Argumenta sirina in barva lahko izpustimo.
• risar.nakljucne_koordinate() vrne naključne koordinate (x, y) znotraj okna.
• risar.nakljucna_barva() vrne naključno barvo, ki jo lahko uporabite za argument barva.
• risar.stoj() ustavi izvajanje programa (poklicati ga je potrebno na koncu programa, sicer se okno takoj zapre).

Napišite program, ki nariše 100 črt naključnih barv in naključne širine med 2 in 20 (uporabite lahko random.randint) med naključnimi koordinatami.

2. Besede

Vaja iz zanke in spremenljivk.

Risar ima tudi funkcijo - risar.besedilo(x, y, s, pisava="Arial", velikost=20, barva=risar.bela), ki na podanih koordinatah s podano barvo izpiše podano besedilo.

Ima tudi konstanti

• risar.maxX in risar.maxY, ki vrneta širino in višino okna v enakih enotah, kot so koordinate, ki jih podajamo funkcijam, kot sta crta in besedilo.

Datoteka krst-zacetek.txt vsebuje začetek pesnitve nekega prešernega pesnika. Preberite vse besede in jih izpišite z naključnimi barvami in velikostmi na naključnih koordinatah. (Nasvet: namesto nakljucne_koordinate uporabite randint in jih odmaknite za 50 točk od spodnjega roba, od desnega pa za 30-kratnik števila črk.)

Glavni izziv bo razbiranje besed. Tistim, ki to znajo narediti z regularnimi izrazi predlagam, da vseeno poskusijo brez.

Al' nek znak c je črka ali ločilo,
pove nam c.isalpha().

3. Oblak besed (no, bolj roj)

Tule bomo malo ponavljali slovarje in urejanje.

V krst-celoten.txt najdete celotno pesnitev, od Valjuna, ki bije krvavi boj, do Bogomila, ki vrne se k očeti in Črtomira ne vidi več na sveti.

Storite podobno kot v prejšnji nalogi, vendar - izpustite besede, krajše od štirih črk, - vsako besedo izpišite le enkrat, - velikost pisave naj bo enaka osemkratniku številu pojavitev besede, - besede izpisujte od redkejših proti pogostejšim.

Nasvet: spoprijateljite s tipom po imenu collections.Counter.

4. Mehurčki

Zdaj pa vaja iz seznamov in zank z malo bolj zanimivimi pogoji.

Risar ima tudi funkcijo

• risar.krog(x, y, r, sirina=1, barva=bela), ki nariše krog s središčem v (x, y) in polmerom r.

Narišite tisoč krogov s širino črte 3. Postopek naj bo takšen. Za vsak krog si izberete naključne koordinate, ki ne ležijo znotraj nobenega od obstoječih krogov. Nato si izberite naključen polmer med 10 in 50, ki ga potem po potrebi še zmanjšajte, tako da ta krog ne bo sekal nobenega od že narisanih krogov.

Matematika: dva kroga se sekata, če je razdalja med njima, $\sqrt{(x_0 - x_1)^2 + (y_0 - y_1)^2}$ manjša od vsote njunih polmerov. Torej mora biti polmer drugega kroga, $r_1$ manjši od $\sqrt{(x_0 - x_1)^2 + (y_0 - y_1)^2} - r_0$.

5. Krogi v krogih

Lahko pa naredimo tako: če je središče kroga znotraj drugega kroga, bo notranji pač primerno manjši, da ne bo sekal zunanjega.

Za začetek narišite kroge z belo barvo; pozabavajte se le s primernimi polmeri.

Ker pa ima risar tudi funkcijo

• risar.barva(r, g, b), ki vrne barvo s komponentami R, G in B (med 0 in 255),

naj bodo notranji krogi modrikasti. Če zunanji krogi so beli (risar.bela oziroma risar.barva(255, 255, 255)). Če se krog nahaja znotraj enega kroga, je barve risar.barva(192, 192, 255), če je znotraj kroga, ki se nahaja znotraj kroga, je barve risar.barva(128, 128, 255), če je gnezden trikrat risar.barva(64, 64, 255), če še globlje pa risar.barva(0, 0, 255). Z drugimi besedami, komponenti R in G sta enaki $2^{8-z}$, kjer $z$ pove, kako globoko je zagnezden krog, vendar ne več kot 255 in ne manj kot 0.

6. Pokanje mehurčkov

Zdaj pa se bomo spomnili, kako brisati stvari iz seznamov. Ker mehurčki, realno, pokajo.

Risarjeve funkcije vračajo rezultate. risar.krog vrne objekt, ki predstavlja krog, zato ga boste v tej nalogi najbrž poklicali s krog = risar.krog(x, y, r, sirina=3) in ga shranili v seznam, v katerem že zdaj beležite x, y in r.

Risar ima tudi funkcijo

• risar.odstrani(element), ki odstrani podani element (recimo krog).

Na osnovi prejšnjega programa napiši novega, ki deluje tako, da si izbere koordinate in polmer kroga (med 10 in 30). Če novi krog seka katerega od obstoječih, obstoječi krogi počijo.

(Če se animacija zatika, kliknite sliko.)

7. "A ti screensaver delaš?"

... je gledaje program izrisujoč sliko iz predprejšnje naloge rekel v sobo vstopivši podmladek.

Že prejšnja bi lahko bila screensaver, tule pa še je eden. V sliki na desni je polmer krogov med 10 in 200 pikslov, barva je risar.barva(c, c, 255), kjer je c naključno število med 0 in 255. Pomembno pa je tole: krogov je največ 500. Ko jih je več, po vsakem risanju novega kroga pobrišemo najstarejši krog.

8. Trikotniki v trikotniku. Večkrat.

Smo razpoloženi za malo rekurzije?

Potem bomo vsekakor narisali trikotnik z oglišči v (10, 475), (537, 475) in (271, 10). Vanj bomo vrisali trikotnik. Nato bomo v vsakega od zunanjih treh trikotnikov vrisali nov trikotnik. To bomo ponavljali, dokler stranice ne bodo manjše od 30. Takšnih ne delimo več.

To poznamo pod imenom trikotnik Sierpinskega.

Da ne bi kdo obupal zaradi matematike: koordinati središča daljice so pač na sredi med krajiščema. Manj učeno: če je imamo stranico trikotnika, ki gre od $(x_a, y_a)$ do $(x_b, y_b)$, je središče te stranice v $(x_a + x_b) / 2, (y_a + y_b) / 2$.

Kako pa boste vedeli, ali ima trikotnik stranice krajše od 30? Preprosto: ena stranica je vedno vodoravna. Izračunajte razliko med njenima koordinatama $x$.

Posnetek na desni je upočasnjen, da je postopek očitnejši.

9. Štirje krogi

Smo razpoloženi za še malo rekurzije?

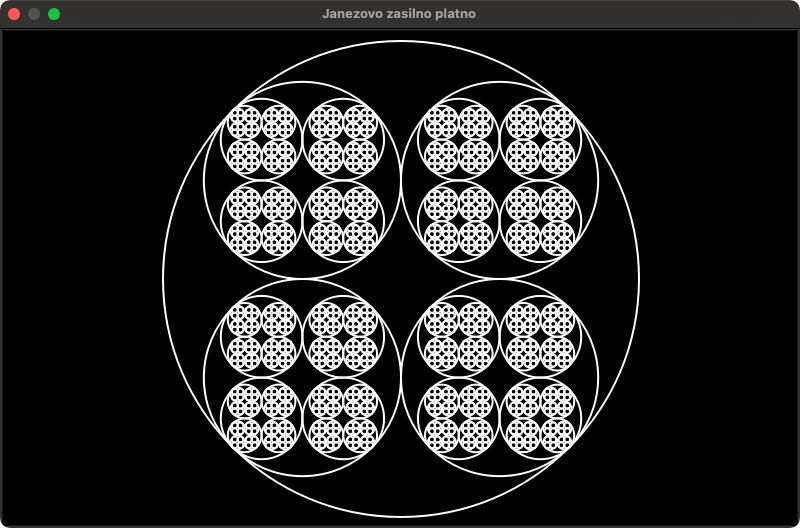
V tem primeru v sredino platna narišimo krog s polmerom risar.maxY / 2 - 10. Vanj vrišemo štiri kroge, kot kaže slika. V vsakega od njih vrišemo štiri kroge ... in tako naprej do globine 5.

Pri tem vas bo neizbežno zanimalo, kakšne so koordinate središča notranjega kroga in njegov polmer. Seveda vas vabim, da to doženete same, kdor raje ne bi, pa lahko pogleda odpre spodnji kvarnik.

10. Spirala

Tule pa jaz programiram, vi pa izbrskate nekaj novega o Pythonu in ponovite nekaj, kar boste tako ali tako potrebovali pri izpitu iz matematike.

Zakaj spodnji program nariše sliko na desni?

import risar

cx, cy = risar.maxX / 2, risar.maxY / 2
x0 = 1 + 0j
while abs(x0) < cy:
    x1 = x0 * (1 + 0.05j)
    risar.crta(cx + x0.real, cy + x0.imag,
               cx + x1.real, cy + x1.imag, 
               sirina=3)
    x0 = x1

risar.stoj()

Tule pa je še nekaj, kar sem sicer pripravil za ne-računalnikarje, vendar tudi računalnikarjem ne bo koristilo, če malo ponovijo branje datotek. :)

1. Krogi po navodilih

V datoteki slika1.csv je seznam koordinat krogov. Narišite kroge s polmerom 3 in središči na koordinatah, zapisanih v datoteki.

2. Črte po navodilih

Povežite kroge s črtami debeline 3. Kaj se izriše?

3. Več črt po navodilih

Zdaj pa storite isto s podatki iz datoteke slika.csv. Videli boste, da le-ta vsebuje prazne vrstice. Tam je potrebno črto prekiniti in začeti risati znova. (Za začetek lahko poskusite prazne vrstice samo preskočiti, pa boste hitro videli, v čem je vic.)

Risanje krogov lahko tudi ukinete in rišete samo črte.

4. Črte po vrstah

Datoteka slika-po-vrstah.csv vsebuje isto reč, le da je vsaka črta v svoji vrstici. (Le poglejte jo, pa vam bo jasno.) Narišite isto sliko, vendar tako, da uporabite to datoteko.

5. Relativne črte

Nismo še brez idej. Datoteka relativna.csv je podobna prejšnji, vendar sta le prvi koordinati absolutni. Vse nadaljnje povedo, za koliko se moramo premakniti od prejšnje koordinate.

6. Funkcije

Morda ste opazili, da se precej vrstic razlikuje le v prvi, absolutni koordinati, relativne pa so enake.

Zakaj ne bi tedaj najprej definirali vseh oblik, kot nekakšne "funkcije", ki bi vsebovale le relativni del koordinat, ne pa tudi začetne. Nato bi te "funkcije" "poklicali", tako da bi navedli njihove začetne koordinate, takole:

podstavek: 0,65,0,-15,31,6,1,27,-46,8,-60,0,-14,-15,6,-26,25,-1,0,16,1,-63
smreka: -25,-12,6,40,-51,-40,9,26,-14,23,-33,-40,1,20,-22,28,-19,-48,-7,23,-38,35,18,-58,-16,-33,-53,50,50,0,-17,32,-33,31,-39,16,58,-10,42,-17,22,39,22,-33,30,34,14,-46,24,19,14,29,0,18,24,-73,28,41,40,10,-33,-59,67,34,-67,-73,28,-1,-38,-26,-14,-37,-32,-61,15,41,-27,-20,11,29,-3,22,-31,-45,-12,38,-15,-26,-23,26,3,-33,-45,44,-1,-13,-36,1,62,-64,-12,-1,36,-22,-13,29,21,-23,8,27,7,-26,26,23,-6,-27,25,14,20,2,-36,-30,-27,-76,-23,63,-36,38
zvezda: 6,-13,5,12,8,1,-8,6,5,12,-12,-8,-10,8,5,-9,-9,-10,10,1
velika-zvezda: 4,17,-11,-8,-11,7,3,-17,-12,-5,13,-2,8,-14,4,14,11,1,-9,7
krog: -12,6,0,9,11,6,10,-9,-9,-12
trikotnik: -7,-11,9,-8,9,10,-11,9

podstavek na 425,362
smreka na 498,272
zvezda na 274,218
zvezda na 429,158
zvezda na 393,229
zvezda na 268,361
zvezda na 422,311
zvezda na 343,162
velika-zvezda na 398,33
krog na 358,216
krog na 439,221
krog na 255,288
trikotnik na 365,333
trikotnik na 487,385
trikotnik na 380,180

Napišite program, ki nariše sliko po navodilih iz takšne datoteke (slika-funkcije.txt).