Čebelji let
Testi
Testi: testi-cebelji-let.py
Obvezna naloga
Napiši funkcijo risi_pot(pot), ki nariše čebeljo pot. Pot
prejme, kot smo navajeni, v obliki niza, sestavljenega iz črk R, L, D in U.
Vsaka črka pomeni pomik za 10 (karkoli že pomenijo te enote - ni pomembno).
Pot se začne na koordinatah (0, 0).
Tako mora risi_pot("RD") narisati črto od (0, 0) do (10, 0)
in od (10, 0) do (10, 10). Klic risi_pot(""RRDRDLLUL") nariše

Dodatna naloga
Napiši podobno funkcijo risi_prosto_pot(pot), pri kateri
posamezen korak ni nujno dolg 10, temveč vsakemu znaku za smer (R, L, U, D)
sledi številka. Tako mora risi_prosto_pot("R23D5") nariše črto
od (0, 0) do (23, 0) in od (23, 0) do (23, 5). Klic
risi_prosto_pot("R1R12D8R4D50L2L12U5R42") nariše
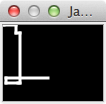
Pazi: število je lahko eno-, dvo- ali trimestno. Znajdi se, kakor veš in znaš.
Rešitev
Obvezna naloga
Naloga zahteva praktično isto kot naloga izpred štirinajstih dni: imamo čebelo, dobimo pot, gonimo čebelo po tej poti ... novo je le, da tokrat ne seštevamo kakih dobičkov, temveč ob vsakem premiku narišemo še črto.
Dodatna naloga
Najtežje pri dodatni nalogi ni risanje - to je pravzaprav trivialno,
komaj kaj težje od onega v obvezni nalogi - temveč branje poti. Za začetek
bomo napisali funkcijo, ki razbije pot na korake: iz, recimo, poti podane z
nizom "R42D13L8" bo naredila seznam
[("R", 42), ("D", 13), ("L", 8)].
Niz pot se bo vedno začel s črko. Postavimo i
na prvo števko in ga povečujemo toliko časa (notranji while),
dokler ne pridemo do konca niza ali do znaka, ki ni števka. Potem vemo,
pot[0] je znak, ki predstavlja smer, vse od 1 do i
(brez i) pa so števke, ki povedo dolžino. V seznam torej dodamo
prvo črko in dolžino.
Nato skrajšamo pot: odbijemo vse do i-tega znaka, kjer se
začne opis naslednjega koraka.
Zunanja zanka while teče, dokler ne zmanjka poti.
Rešitev je precej Pythonovska. V drugih jezikih bi pogotejše videli nekaj takšnega:
Tu si namesto, da bi po vsakem izločenem koraku odrezal niz, zapomnim, do
kje sem že prišel (j). Z i tako ne grem od
1 temveč od j + 1 in v pot ne dodajam
(pot[0], int(pot[1:i])) temveč
(pot[j], int(pot[j+1:i])). Bistvena razlika med programoma
je v tem, da znam prvega v prvem poskusu sprogramirati brez napake, pri
drugem pa se prej trikrat zmotim.
Zdaj ko imamo to funkcijo - takšno ali drugačno -, je preostanek preprost.
